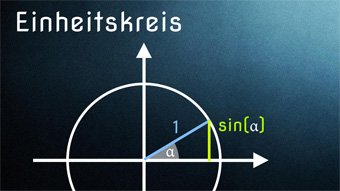
Sinus, Kosinus und Tangens hatten wir bereits am rechtwinkligen Dreieck kennengelernt. Jetzt gehen wir einen Schritt weiter.
Wir legen Sinus, Kosinus und Tangens an einem Kreis fest, der den Radius 1 hat. Daher spricht man vom „Einheitskreis“.
Welche Vorteile sich dadurch ergeben, sehen wir im Folgenden.
Zuerst erinnern wir uns daran, dass die Winkel in einem rechtwinkligen Dreieck nie größer als 90° sein können:
Auch sind Sinus und Kosinus für Winkel bis 180° in allgemeinen Dreiecken definiert, jedoch können die Winkel in einem allgemeinen Dreieck nie größer als 180° sein.
Sinus und Kosinus für beliebige Winkel
Wenn wir uns einen Kreis zu Hilfe nehmen, können wir jedoch beliebige Winkel festlegen und damit auch die (Ko)Sinuswerte und Tangenswerte für beliebige Winkel bestimmen.
Um dies zu erreichen, zeichnen wir ein Koordinatensystem und einen Kreis. In diesen Kreis legen wir ein rechtwinkliges Dreieck, von dem ein Punkt B der Mittelpunkt des Kreises ist und ein Punkt A auf der Kreislinie liegt. Der dritte Punkt C befindet sich auf der x-Achse, und zwar dort, wo das Lot vom Punkt A die x-Achse trifft:
An diesem rechtwinkligen Dreieck können wir alle drei trigonometrischen Funktionen Sinus, Kosinus und Tangens festlegen. Wir erkennen, dass wir ein Referenzdreieck in jedem der vier Quadranten einzeichnen können:
Referenzdreieck im II. Quadranten:
Referenzdreiecke in allen vier Quadranten:
Was weiterhin auffällt ist, dass wir auch negative Werte für Sinus, Kosinus und Tangens erhalten, wenn x-Wert oder y-Wert negativ sind.
Referenzwinkel am Kreis
Wie wir bei Sinus und Kosinus bei allgemeinen Dreiecken gesehen haben, erhalten wir für einen Winkel zwischen 90° und 180° folgendes Dreieck mit Referenzwinkel, nun dargestellt im Einheitskreis:
Dabei ist der Sinuswert von Alpha: sin(α) = sin(β) und β = 180° - α, sodass wir festhalten können: sin(α) = sin(180° - α)
Aufgrund solcher Identitäten können sin, cos und tan für beliebige Winkel festgelegt werden. Mehr zu den Identitäten hier.
Definition Einheitskreis
Beim Einheitskreis ist der Radius des Kreises 1 Einheit lang. Das hat den Vorteil, dass wir die Sinus- und Kosinuswerte direkt an den x- und y-Werten der Dreiecksseiten ablesen können.
Mit dem Radius 1 (der die Hypotenuse des Dreiecks ist) ergibt sich:
\( \textcolor{#00F}{\sin(α)} = \frac{GK}{HK} = \frac{GK}{1} = \textcolor{#00F}{GK} \\[1ex] \textcolor{#F00}{\cos(α)} = \frac{AK}{HK} = \frac{AK}{1} = \textcolor{#F00}{AK} \\[1ex] \tan(α) = \frac{GK}{AK} \)
Weiter geht es mit dem Artikel: Sinus und Kosinus am Einheitskreis