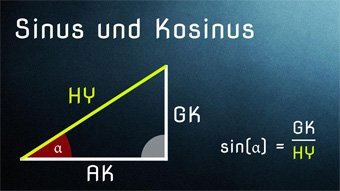
Wenn wir uns ein Dreieck nehmen und die Winkel gleich lassen, jedoch die Größe des Dreiecks ändern (die Seitenlängen verändern sich), stellen wir fest:

dass das Verhältnis von Gegenkathete zur Hypotenuse immer gleich bleibt.
Zur Erinnerung: Um ein Verhältnis zu bilden, dividiert man, in unserem Fall die Gegenkathete durch die Hypotenuse, also GK:HY bzw. in Bruchschreibweise: GK/HY.
Für das obige Beispiel haben wir bei einem Winkel von 30° die Verhältnisse:
GK/HY = 3 cm/6 cm = 4 cm/8 cm = 5 cm/10 cm = 0,5
Also immer 0,5 und zwar egal, welche Dreiecksgröße wir wählen.

Dieses Verhältnis nennen wir den Sinuswert und schreiben: sin(30°) = 0,5
Die Formel für den Sinus lautet allgemein:
sin(α) = Gegenkathete/Hypotenuse
Dieser Wert gibt uns an, wie lang die Gegenkathete im Vergleich zur Hypotenuse ist.
Haben wir einen Winkel von 30° und wissen wir, die Hypotenuse ist 8 cm lang, so können wir aufstellen:
sin(30°) = 0,5 = GK/HY
Damit GK = 0,5·HY
Die Gegenkathete ist also 0,5 mal so lang wie die Hypotenuse (0,5 = 50 % von ihrer Länge).
Mit den Werten: GK = 0,5·HY = 0,5·8 cm = 4 cm (als Länge der Gegenkathete).