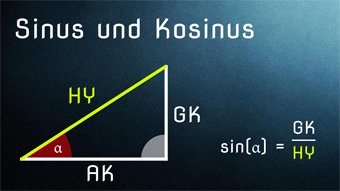
Für jeden Winkel gibt es einen Sinuswert. Die folgende Tabelle zeigt uns die Sinuswerte von 0° bis 90° in Zehnerschritten:
| Winkel | Sinuswert | Sinuswert gerundet |
|---|---|---|
| 0° | 0,000 | 0,000 |
| 10° | 0,17364817766693 | 0,174 |
| 20° | 0,342020143325669 | 0,342 |
| 30° | 0,500 | 0,500 |
| 40° | 0,642787609686539 | 0,643 |
| 50° | 0,766044443118978 | 0,766 |
| 60° | 0,866025403784439 | 0,866 |
| 70° | 0,939692620785908 | 0,940 |
| 80° | 0,984807753012208 | 0,985 |
| 90° | 1,000 | 1,000 |
Bei einem Winkel von 0° hat die Gegenkathete eine Länge von 0. Wir berechnen sin(0°) = GK/HY = 0/HY = 0.
Daher ist sin(0°) = 0.
Bei einem Winkel von 90° ist die Gegenkathete genauso lang wie die Hypotenuse. Das heißt, wir berechnen sin(90°) = (GK)/HY = (HY)/HY = 1.
Daher ist sin(90°) = 1.