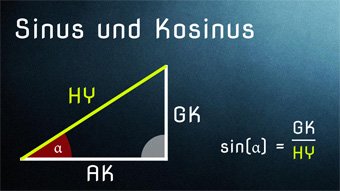
Wenn ihr eine Aufgabe bekommt, bei der eine Seite des rechtwinkligen Dreiecks bekannt ist und ein Winkel, dann könnt ihr die unbekannten Seiten bestimmen.
Beispielaufgabe: Gegeben sind Winkel α = 70° und Seite a = 5 cm
Lösungschritte:
1. Zuerst das Dreieck anschauen, wo liegen der Winkel α und die Seite a.

2. Wir sehen, dass Seite a dem Winkel α gegenüberliegt, also ist Seite a die Gegenkathete von Winkel α. Wir kennen also Winkel und Gegenkathete und nehmen daher den Sinus.
3. Stellen wir auf: \( \sin(α) = \frac{GK}{HY} \)
4. Setzen wir die Werte ein und rechnen aus:
\( \sin(α) = \frac{\text{GK}}{\text{HY}} \\ \sin(α) = \frac{a}{c} \\ \sin(70°) = \frac{5 \text{cm}}{c} \qquad | \text{ nun stellen wir die Gleichung um} \\ \sin(70°) = \frac{5 \text{cm}}{c} \qquad | ·c \\ \sin(70°) · c = 5 \text{cm} \qquad | : \sin(70°) \\ c = 5 \text{cm} : \sin(70°) \)
Das in den Taschenrechner eingeben: 5 * SIN 70 (darauf achten, dass DEG und nicht RAD eingestellt sind)
c = 5,3208888623795607… cm
c ≈ 5,321 cm
Die Eingabe sei kurz am Taschenrechner gezeigt (dort seht ihr auch, wo man den Modus DEG einstellen muss):

DEG steht übrigens für DEGree und meint das Gradmaß (Kreis in 360° eingeteilt). RAD steht für RADiant und meint das Bogenmaß (Kreis in 2·π rad eingeteilt).
Jetzt haben wir Seite a und c sowie Winkel α vorzuliegen. Wir wissen außerdem, dass Winkel γ = 90° ist. Winkel β können wir über den Innenwinkelsummensatz bestimmen:
5. Winkel β berechnen
α + β + γ = 180°
70° + β + 90° = 180°
β = 180° - 70° - 90°
β = 20°
Fehlt nur noch die Seite b. Hier können wir nun wieder den Sinus nehmen, und zwar (blickt auf die Dreiecksgrafik oben) ist b die Gegenkathete von Winkel β. Die Hyoptenuse c ist uns bekannt. Wir stellen also auf:
6. Seite b berechnen:
sin(β) = \( \frac{GK}{HY} \)
sin(β) = \( \frac{b}{c} \)
sin(20°) = \( \frac{b}{ 5,321 \text{cm} } \) | · 5,321 cm
b = sin(20°)·5,321 cm
Das in den Taschenrechner wie folgt eingeben:
SIN 20 * 5,321
(Unbedingt darauf achten, dass DEG und nicht RAD eingestellt ist.)
Als Ergebnis erhalten wir:
b = 1,819889182635883… cm
b ≈ 1,82 cm
7. Fertig, wir haben alle Winkel und Seiten bestimmt:
α = 70°, β = 20°, γ = 90°, a = 5 cm, b = 1,82 cm, c = 5,321 cm
8. Wer sich unsicher ist, gibt drei der berechneten Werte im Dreiecksrechner ein und prüft, ob sich die anderen Werte ergeben. Dies ist bei uns der Fall, wir haben richtig gerechnet.
Alternativ lassen sich mit dem Kosinus die Berechnungen für die Dreiecksseiten ausführen.