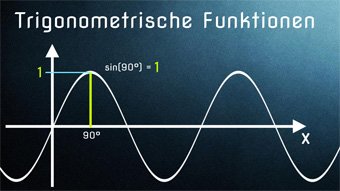
Wir können uns die Periodizität auch vor Augen führen, wenn wir den Sinusgraphen direkt in den Einheitskreis einzeichnen. Wenn wir von 0° zu 90° gehen, sehen wir, dass wir den Graphen oben bei 1 erreichen. Also Sinus von 90° ist 1. Und gehen wir jetzt zu 180°, nimmt unser Sinuswert ab und wir erreichen die 0. Gehen wir weiter, kommen wir bei 270° zum Sinuswert -1 und bei 360° wieder zur 0. Hier können wir jetzt auch 360° hinzuaddieren und sehen, dass sich für die höheren Winkel der gleiche Verlauf ergibt. Oder aber, wir könnten 360° abziehen und hätten auch den gleichen Verlauf.
Mit eingezeichneter Periode sieht das so aus (periodische Schwingung):

Der Sinusgraph ist periodisch, denn all seine Werte wiederholen sich jede 360°.
Einheitskreis entlang Sinuskurve
Wir haben uns überlegt, wie wir noch besser den Zusammenhang zwischen Einheitskreis und Sinuskurve darstellen können. Dabei ist folgendes Programm entstanden, das euch deutlich zeigt, wie die Höhen des Einheitskreises zu den Sinuswerten im Koordinatensystem werden: