Damit wir das Thema verstehen können, müssen wir den Einheitskreis verstanden haben. Dort haben wir gelernt, wie man Sinus und Kosinus für alle beliebigen Winkel definieren kann. Den Einheitskreis benötigen wir nun, um die trigonometrischen Funktionen darstellen zu können.
Die trigonometrischen Funktionen nennt man auch „Winkelfunktionen“. Zu ihnen gehören Sinusfunktion, Kosinusfunktion und Tangensfunktion (sogenannte „elementare trigonometrische Funktionen“).
Was ist eine Funktion? (Wiederholung)
Bei den linearen Funktionen hatten wir den Funktionsbegriff kennengelernt. Bei der Funktionsgleichung f(x) = 2·x erkennen wir, dass der Name der Funktion „f“ ist.
Zudem ist hier eine Variable „x“ definiert, für die ein Wert eingesetzt wird, und darauf folgt (nach dem =) die Berechnung der Funktion folgt. Schließlich kommt ein y-Wert heraus.
Daraus ergeben sich dann Wertepaare x und y, die unsere Punkt-Koordinaten P(x|y) darstellen. Mit diesen Punkten können wir den Graphen der Funktion zeichnen.
Eine Funktion meint also eine Zuordnung, bei der jeder x-Wert einen y-Wert zugeordnet bekommt.
Was ist die Sinusfunktion?
Bei der Sinusfunktion haben wir kein f(x), sondern ein sin(x). sin ist der Name der Funktion.
Bei diesem sin(x) setzen wir einen x-Wert ein und ein Sinuswert kommt heraus. Das x ist dabei ein Winkel.
Denken wir an den Einheitskreis:
Sinus von 0° hat die Höhe 0.
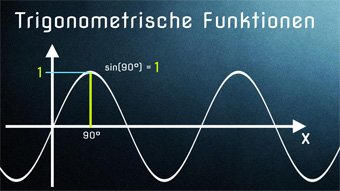
Sinus von 90° hat die Höhe 1.
Das heißt, jede Gradzahl (0°, 90°) erhält einen Sinuswert (0, 1) zugeordnet. Diese Wertepaare ergeben x- und y-Koordinaten für unsere Punkte.
sin(0°) = 0 → P1 (0°|0)
sin(90°) = 1 → P2 (90°|1)
Macht man dies für viele Punkte, so ergibt sich die Sinusfunktion:
~plot~ sin(x*pi/180);{0|0};{90|1};[[-400|600|-1,2|1,2]];noinput;;nolabels ~plot~
Bitte achtet darauf, dass wir für x immer Winkelwerte einsetzen, also ein Gradmaß wie 90°. Die Angabe in Bogenmaß wie 1 rad lernen wir später kennen.
Rufen wir uns den Einheitskreis in Erinnerung und schauen, wie wir mit ihm auf einfache Weise den Graphen der Sinusfunktion erstellen können.
Weiter geht es mit: Vom Einheitskreis zur Sinusfunktion