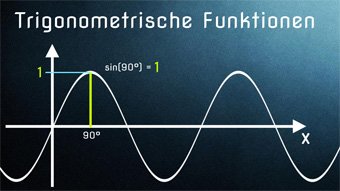
Zur Erinnerung: Tangens ergibt sich aus dem Verhältnis Sinus zu Kosinus. Zum Beispiel: tan(45°) = sin(45°) / cos(45°) ≈ 0,707 / 0,707 = 1. Wir schreiben also tan(45°) = 1.
Tangenswerte können positiv und negativ sein und im Gegensatz zu Sinus und Kosinus alle beliebigen Werte annehmen.
Als nächstes wollen wir die Tangenswerte den entsprechenden Winkeln zuordnen.
Graph der Tangensfunktion
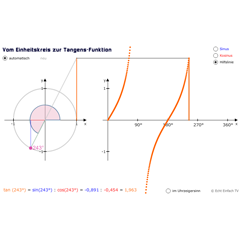
Führen wir uns die Tangenswerte vor Augen, denken wir daran stets an den Einheitskreis:
Tangens von 0° ist 0.
Wenn wir zu 45° gehen, dann haben wir Tangens von 45° ist 1.
Wenn wir über 45° gehen, erhalten wir immer höhere Werte.
Bei 90° ist der Tangens nicht definiert, also tan(90°) = n.d. (sog. „Definitionslücke“).
Wenn wir über 90° gehen, bekommen wir negative Werte. Zum Beispiel tan(135°) = -1.
Bei tan(180°) erreichen wir den Tangenswert 0.
tan(270°) ist auch wie tan(90°) nicht definiert.
Zeichnen wir basierend auf diesen Ausführungen den Graphen der Tangensfunktion in ein Koordinatensystem ein:

Wie wir erkennen, erhalten wir immer diese geschwungenen Linien, die uns die Tangenswerte wiedergeben. Anders als bei den Graphen für Sinus und Kosinus haben wir hier keine Welle, sondern einen leicht geschwungenen nach oben gehenden Graphen, dessen Wert 0 ist bei 0°, 180° und 360°. Die Periode liegt hier zwischen 90° und 270°. Die Periode ist im Vergleich zu Sinus und Kosinus kürzer. Sie beträgt 180°, und bei Sinus und Kosinus 360°.
Periode beim Tangens
Auch beim Tangensgraphen erkennen wir eine Periodizität. Jeder Winkel α erhöht um +180° hat den gleichen Tangenswert. Die Tangenswerte wiederholen sich, die Tangensfunktion ist periodisch.
Definitionslücken bei Tangens
Wir sehen beim Tangensgraphen auch die sogenannten Definitionslücken, also die Stellen, wo sich kein y-Wert zuordnen lässt. Beim Einheitskreis hatten wir gelernt, dass wir für tan(90°) keinen Wert haben. Er war nicht definiert, da tan(90°) = sin(90°) / cos(90°) = 1 / 0 = nicht definiert. Gleiches bei tan(270°).
Sobald wir auf ein „nicht definiert“ stoßen, können wir keinen Wert beim Graphen einzeichnen, wir sagen Definitionslücke dazu. Bei 90° und bei 270° haben wir keinen Wert zum Eintragen.