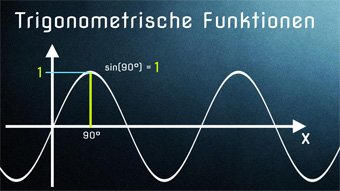
Die trigonometrischen Funktionen nennt man auch „Winkelfunktionen“. Zu ihnen gehören Sinusfunktion, Kosinusfunktion und Tangensfunktion (sogenannte „elementare trigonometrische Funktionen“).
Der Verlauf des Sinusgraphen ist nicht „rund“ wie beim Kreis, sondern geschwungen.
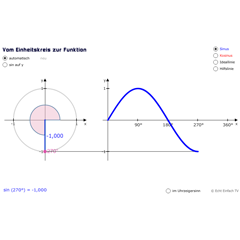
Nehmen wir uns ein Beispiel, das auch den Verlauf des Graphen erklärt. Stellen wir uns vor, im Zentrum des Koordinatensystems befindet sich ein Ball, den wir nach oben werfen. (Damit es physikalisch korrekt ist, befestigen wir eine Feder am Ball, die ihn wieder zurücktreibt, wenn er ganz oben ist, die Gravitationskraft vernachlässigen wir). Die x-Achse soll jetzt nicht die Winkel wiedergeben, sondern den zeitlichen Verlauf (z. B. in Millisekunden). Der Ball wird eine gewisse Höhe erreichen und dann zurückkommen durch die Kraft der Feder.

Zuerst ist der Ball sehr schnell, dann wird er langsamer, und ganz oben verharrt er bei 1. Er hat sozusagen 100 % seiner Wurfhöhe erreicht. Danach kehrt er wieder zurück und wird, je näher er der 0 kommt, schneller werden. Dieses kleine Beispiel soll zeigen, warum der Sinusgraph so geschwungen ist.
Der Graph der Sinusfunktion verrät uns, um wie viel der Sinuswert (im Beispiel die Ballhöhe), zunehmen wird von einem Winkel zu einem anderen Winkel (oder von einer Millisekunde zur nächsten Millisekunde).
Denn wenn der Ball die Hälfte der Zeit fliegt (bzw. von 0° zu 45°), heißt das nicht, dass er die Hälfte des Weges nach oben geflogen ist. Die Höhen unterscheiden sich!
Gehen wir zum Beispiel von 0° zu 20°, also sin(0°) = 0 und sin(20°) = 0,342, dann sehen wir, dass 34,2 % der Strecke erreicht ist.
Prüfen wir die gleiche Winkelspanne (bzw. Zeitverlauf) von 70° zu 90° mit sin(70°) = 0,940 (bei 70° haben wir 94 % der Strecke erreicht) und sin(90°) = 1, also 100 % der Strecke.
Das heißt, wir haben von 94 % zu 100 % nur 6 % der Strecke zurückgelegt.
Am Anfang hatten wir 0° + 20° gerechnet und 34 % zurückgelegt. Am Ende hatten wir 70° + 20° gerechnet und eine Höhe von nur 6 % zurückgelegt. Und genau dieses Verhalten beschreibt uns der Graph der Sinusfunktion.
Wichtig: Die Zunahme des Sinuswertes von einem Grad zum nächsten Grad ist unterschiedlich.