Lektion TRI03: Sinussatz und Kosinussatz - Matheretter In diesen Mathe-Videos lernen wir, wie Sinus und Kosinus zur Berechnung von allgemeinen Dreiecken benutzt werden. Hier treffen wir auf den Sinussatz und den Kosinussatz. Auch lernen wir (Ko)Sinuswerte bis 180 Grad kennen!
Matheretter

Lektion TRI03: Sinussatz und Kosinussatz

Inhalte:

  1. Wie ergeben sich Sinussatz und Kosinussatz für allgemeine Dreiecke?
  2. Wie leitet man Sinus- und Kosinussatz her?
  3. Welche Anwendungen in Dreiecken gibt es für beide Sätze?
  4. Wie kommt man auf die Identitäten sin(α) = sin(180-α) und cos(α) = -cos(180-α)?
  5. Wie wird aus dem Kosinussatz der Satz des Pythagoras?
  6. Wie bestimmt man unbekannte Winkel mit Hilfe des Kosinussatzes?
Voraussetzung:
Laut Lehrplan: 9. - 10. Klasse
Videos anschauen › Artikel lesen ›

In der vorigen Lektion haben wir Sinus und Kosinus kennengelernt. Diese können wir nun benutzen, um allgemeine Dreiecke zu berechnen. Hierzu nutzen wir den Sinussatz und den Kosinussatz, die wir in den Videos herleiten. Auch stoßen wir beim allgemeinen Dreieck auf Winkel über 90° bis 180°, für die wir ebenfalls Sinus- und Kosinuswerte bestimmen können.

Sinus+Kosinus bei Dreiecken - Kosinussatz inkl. Herleitung

Herleitung des Kosinussatzes mit Hilfe vom Satz des Pythagoras und dem Kosinus. Bei gegebenen 2 Seiten und eingeschlossenem Winkel kann mit dem Kosinussatz die 3. Dreiecksseite bestimmt werden. Eselsbrücke fürs leichtere Merken der Formel.

Zugriff auf Video nur als eingeloggter Benutzer.

Registrieren Einloggen

Weitere Videos für Kunden:

  • Abo
    Zugriff auf alle Videos
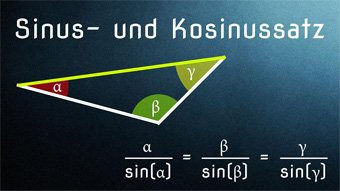
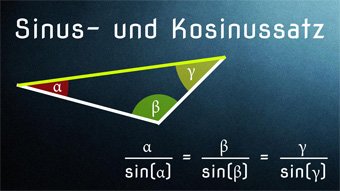
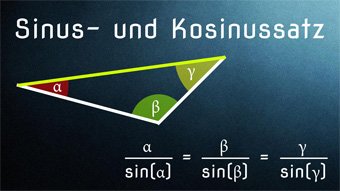
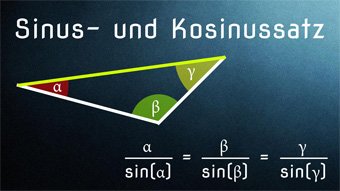
    TRI03-1 Sinus+Kosinus bei Dreiecken - Sinussatz
    Herleitung vom Sinussatz, Berechnen von Beispielen im allgemeinen Dreieck, Seiten und Winkel bestimmen mit Hilfe des Sinussatzes: a / sin(α) = b / sin(β) = c / sin(γ)
  • Abo
    Zugriff auf alle Videos
    TRI03-2 Sinus+Kosinus bei Dreiecken - Sinus u. Kosinus bis 180 Grad
    Höhe des Allgemeinen Dreiecks als Gegenkathete, Sinus-Werte von 90° bis 180°, Identitäten sin(α) = sin(180-α), cos(α) = -cos(180-α), Anwendung Sinussatz am stumpfwinkligen Dreieck.
  • Abo
    Zugriff auf alle Videos
    TRI03-4 Sinus+Kosinus bei Dreiecken - Kosinussatz über Flächen
    In diesem Video leiten wir den Kosinussatz über die Flächenformel her. Abschließend zeigen wir, unter welchen Umständen aus dem Kosinussatz der Satz des Pythagoras wird.
  • Abo
    Zugriff auf alle Videos
    TRI03-5 Sinus+Kosinus bei Dreiecken - Kosinussatz Winkel berechnen
    Anwendung des Kosinussatzes zur Dreiecksberechnung, Ermittlung des unbekannten Winkels aus 3 Dreiecksseiten, Zusammenfassung und Falleinteilung, wann der Sinussatz oder der Kosinussatz anzuwenden ist.

Alle Videos bestellen

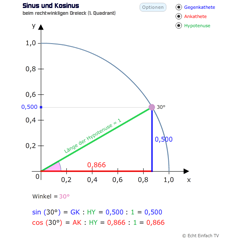  • Sinus und Kosinus im 1. Quadrant
    Sinus und Kosinus im 1. Quadrant
    Lernt die Werte für Sinus und Kosinus von 0 bis 90 Grad. Der Wert für Sinus steht an der Gegenkathete, der Wert für Kosinus an der Ankathete. Nutzt auch die Koordinaten des Punktes auf dem Kreisbogen.
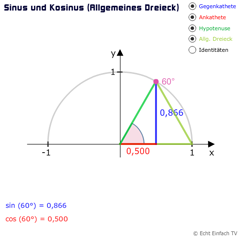  • Sinus und Kosinus (Allgemeines Dreieck)
    Sinus und Kosinus (Allgemeines Dreieck)
    Mit der Dreieckshöhe als Gegenkathete können wir Sinus und Kosinus im allgemeinen Dreieck anwenden. Wir nutzen ein Referenzdreieck für Winkel über 90 Grad am Halbkreis sowie Identitäten.
  • Sinussatz zur Dreiecksberechnung
    Sinussatz zur Dreiecksberechnung
    Mit diesem Programm können beliebige Dreiecke mit Hilfe des Sinussatzes berechnet werden. Hierzu sind nur 3 Werte anzugeben. Zusätzlich können Höhen und Fläche angezeigt werden.
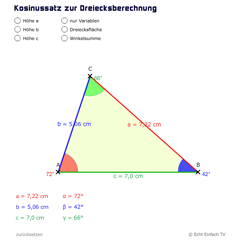  • Kosinussatz zur Dreiecksberechnung
    Kosinussatz zur Dreiecksberechnung
    Mit diesem Programm können beliebige Dreiecke mit Hilfe des Kosinussatzes berechnet werden. Hierzu sind nur 3 Werte anzugeben. Zusätzlich können Höhen und Fläche angezeigt werden.
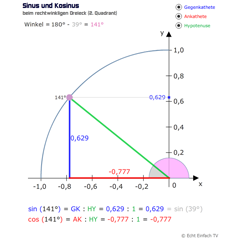  • Sinus und Kosinus im 2. Quadrant
    Sinus und Kosinus im 2. Quadrant
    Die Werte für Sinus und Kosinus von 90 bis 180 Grad können hier gelernt werden. Der Wert für Sinus ist die Länge der Gegenkathete, der Wert für Kosinus die Länge der Ankathete.
  • Sinussatz am Dreieck berechnen
    Sinussatz am Dreieck berechnen
    Einfach die Wert für das Dreieck eingeben, alle Ergebnisse werden automatisch berechnet. Sinussatz ist a/sin(α) = b/sin(β) = c/sin(γ)

Zugriff auf alle Programme

Hier findest du 1 Arbeitsblatt, mit dem du dein Wissen testen kannst.