Lektion G13: Termumformungen - Matheretter Wir lernen, wie man das Ausmultiplizieren, Ausklammern und die Binomischen Formeln benutzen kann, um Terme umzuformen und Gleichungen zu lösen.
Matheretter

Lektion G13: Termumformungen

Inhalte:

  1. Was ist der Unterschied zwischen Term und Gleichung?
  2. Was bedeutet die Kurzschreibweise 2x?
  3. Wie kann man Terme mit Klammern ausmultiplizieren?
  4. Wie multipliziert man Klammern miteinander?
  5. Wie muss man ausklammern?
  6. Wie vereinfacht man Terme?
Voraussetzung:
Laut Lehrplan: 8. Klasse
Videos anschauen › Artikel lesen ›

Erinnern wir uns an die Lektion: Terme und Gleichungen. Dort hatten wir die Grundlagen zum Umformen von Termen und Gleichungen kennengelernt. Diese Lektion hier ist eine Fortsetzung des Themas, jedoch formen wir jetzt Terme und Gleichungen mit Variablen um, indem wir Ausmultiplizieren, Ausklammern und die binomischen Formeln zu Hilfe nehmen.

Wenn ihr das Distributivgesetz verinnerlicht habt, wird euch diese Lektion leicht fallen.

Wer an der einen oder anderen Stelle Wissenslücken hat, kann noch einmal in die vorigen Lektionen hineinschauen:

Termumformung - Ausmultiplizieren

Was sind Term und Gleichung, Gleichungen lösen, Kurzschreibweise 2x. Ausmultiplizieren als Anwendung des Distributivgesetzes. Ausmultiplizieren mit Variablen in Klammern. Lösen der Gleichung: 2·(3x+5) = 22 sowie 5·(2x-3) = (3x-4)·4. Wie muss man zwei Klammern miteinander multiplizieren.

Zugriff auf Video nur als eingeloggter Benutzer.

Registrieren Einloggen

Weitere Videos für Kunden:

  • Abo
    Zugriff auf alle Videos
    G13-2 Termumformung - Ausklammern
    Ausklammern und das Distributivgesetz. Ausklammern beim Term 24+10x. Wie finden wir die auszuklammernde Zahl (Primfaktorzerlegung/ggT). Lösen der Gleichung: x²+30x=0. Ausklammern bei Termen: 9a+3, 5xy+10xz und 36c²d+3cd+48cd².
  • Abo
    Zugriff auf alle Videos
    G13-3 Termumformung - Binomische Formeln
    Lösen der Gleichung x²-4x+4=0 mit der Binomischen Formel. Vereinfachen und lösen der Bruchterm-Gleichung: (x²-4)/(x+2)=0. Vereinfachen von Termen: (ab+0,5cd)², (x-1)(x+1)(x+3), (5yx³-5y³x)/(x-y), 25a²b²-225a². Unterschied zwischen Term- und Äquivalenzumformung.

Alle Videos bestellen

Hier findet ihr nochmals die Programme zum Distributivgesetz, zu den Binomischen Formeln, zu Primzahlen und dem ggT:

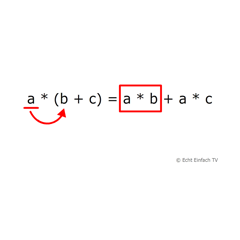  • Distributivgesetz (rechnerisch)
    Distributivgesetz (rechnerisch)
    Die rechnerische Anwendung des Distributivgesetzes animiert dargestellt.
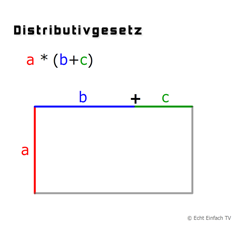  • Distributivgesetz (grafisch)
    Distributivgesetz (grafisch)
    Grafische Darstellung des Distributivgesetzes.
  • Binomische Formel (1)
    Binomische Formel (1)
    Die 1. Binomische Formel wird hier grafisch veranschaulicht. Die Fläche (a+b)² entspricht der Fläche a²+2·ab+b².
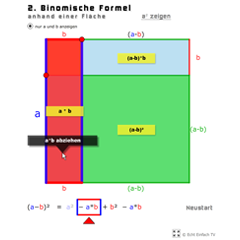  • Binomische Formel (2)
    Binomische Formel (2)
    Die 2. Binomische Formel grafisch in Form von Flächen dargestellt. (a-b)² = a² - 2·a·b + b². Bitte lest euch die Einleitung durch.
  • Binomische Formel (3)
    Binomische Formel (3)
    Die 3. Binomische Formel (a+b)·(a-b) = a² - b² kann mit diesem Programm entdeckt werden. Bitte die Einleitung durchlesen.
  • Primzahlen 2 bis 997
    Primzahlen 2 bis 997
    Die Primzahlen 2 bis 997 grafisch über ihre Längen dargestellt.
  • Größter gemeinsamer Teiler (ggT)
    Größter gemeinsamer Teiler (ggT)
    Der ggT gibt die größtmögliche Zahl an, durch die zwei Zahlen teilbar sind.

Zugriff auf alle Programme