Hexadezimalzahlen in Dezimalzahlen umwandeln

Video

Hexadezimalzahlen in Dezimalzahlen umwandeln

Hexadezimalzahlen in Dezimalzahlen umwandeln

Wir hatten uns die Hexadezimalzahlen bereits angeschaut und gelernt, dass sie mit insgesamt 16 Ziffern 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F gebildet werden.

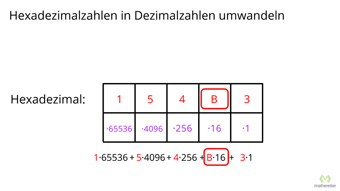
Jede Stelle hat einen „16er-Wert“. Hier ein Beispiel zur Erinnerung:

Diese Stellen müssen wir addieren, um auf den Dezimalwert zu kommen, für das Beispiel:

= 154B3 (hexadezimal)
= 1·65536 + 5·4096 + 4·256 + B·16 + 3·1
= 65536 + 20480 + 1024 + 11·16 + 3
= 65536 + 20480 + 1024 + 176 + 3
= 87219 (dezimal)

Vorgehen

Zur Umwandlung einer Hexadezimalzahl in eine Dezimalzahl gehen wir also wie folgt vor (als Beispiel nehmen wir die Hexadezimalzahl 2A7F):

1. Unter jede Stelle der Hexadezimalzahl den Dezimalwert der Stelle schreiben:

   Hexadezimal:	2	A	7	F
   Dezimal:	4096	256	16	1

   Wir fangen von rechts an mit 1 und versechzehnfachen den Wert jeweils (1, 16, 256, 4096, 65536, 1048576, …).

2. Im nächsten Schritt schreiben wir die Buchstaben A (10), B (11), C (12), D (13), E (14), F (15) mit ihren Dezimalwerten, damit wir damit rechnen können:

   Hexadezimal:	2 (2)	A (10)	7 (7)	F (15)
   Dezimal:	4096	256	16	1

3. Jetzt multiplizieren wir die Werte:

   Hexadezimal:	2 (2)	A (10)	7 (7)	F (15)
   Dezimal:	2·4096	10·256	7·16	15·1

4. Wir addieren alle Werte zusammen und erhalten die gesuchte Dezimalzahl.

   2·4096 + 10·256 + 7·16 + 15·1 = 10 879 (dezimal)

5. Wir können dann wie folgt notieren, im besten Fall mit dem jeweils richtigen Index:

   2A7F₁₆ = 10 879₁₀

Potenzdarstellung

Wenn ihr die Potenzen bereits kennt, dann schreibt die Sechzehnerzahlen stets als Potenzen auf:

A5B₁₆ = A·16² + 5·16¹ + B·16⁰
A5B₁₆ = A·256 + 5·16 + B·1
A5B₁₆ = 10·16² + 5·16 + 11
A5B₁₆ = 2560 + 80 + 11
A5B₁₆ = 2651₁₀