Hexadezimalzahlen

Bei den Dezimalzahlen haben wir zehn Ziffern zur Verfügung. Bei den Binärzahlen haben wir nur zwei Ziffern.

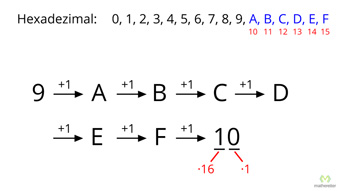
Das Hexadezimalsystem hat 16 Ziffern, und zwar:

0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F

Während wir bei den Binärzahlen weniger Ziffern (zwei) als bei den Dezimalzahlen (zehn) haben (und auf die bekannten Ziffern 0 und 1 zurückgreifen konnten), müssen wir beim Hexadezimalsystem neue Ziffern hinzufügen. Hierbei nimmt man sich die Buchstaben A, B, C, D, E, F zu Hilfe.

Die Hexadezimalzahlen von 0 bis 17 (dezimal) sehen entsprechend so aus:

Hexadezimalsystem	0	1	2	3	4	5	6	7	8	9	A	B	C	D	E	F	10	11
Dezimalsystem	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17

Ein Übertrag kommt also erst nach F zustande:

\( D \xrightarrow[]{\text{+1}} E \xrightarrow[]{\text{+1}} F \xrightarrow[]{\text{+1}} 10 \xrightarrow[]{\text{+1}} 11 \xrightarrow[]{\text{+1}} 12 \)

Und hier aufpassen: Hexadezimal 10 ist dezimal 16. Hexadezimal 11 ist dezimal 17, auch wenn es wie eine 10 bzw. 11 aussieht, so haben sie doch andere Dezimalwerte. Also mit Index geschrieben:

10₁₆ = 16₁₀
11₁₆ = 17₁₀
12₁₆ = 18₁₀
13₁₆ = 19₁₀

Das Wort „Hexadezimal“ kommt übrigens aus dem Griechischen von „hexa“ („sechs“) und „deka“ („zehn“), was also nichts weiter als „sechzehn“ bedeutet.

Stellenwerte

Bei den Hexadezimalzahlen ist der Stellenwert jeder Ziffer 16-mal so hoch wie der Stellenwert der nächsten Ziffer rechts. Bei den Dezimalzahlen ist es 10-mal so hoch.

Wichtig ist, dass wir uns die Dezimalwerte der Buchstaben einprägen:

A = 10, B = 11, C = 12, D = 13, E = 14, F = 15

Dann wissen wir, dass zum Beispiel die Hexadezimalzahl „D3“ folgenden Dezimalwert hat:

D3 (hexadezimal)
= D·16  + 3·1
= 13·16 + 3·1
= 211 (dezimal)

Notation von Hexadezimalzahl und Dezimalzahl

Um kenntlich zu machen, welches Zahlensystem verwendet werden soll, schreibt man einen tiefgestellten Index an die Zahl.

Beispiel Hexadezimalzahl: FF50₁₆. Die tiefgestellte 16 zeigt an, dass es sich um eine Hexadezimalzahl handelt.

Beispiel Dezimalzahl: 1385₁₀. Die tiefgestellte 10 zeigt an, dass es sich um eine Dezimalzahl handelt.

Hexadezimalzahl-Tabelle

Die folgende Tabelle gibt noch mal einen besseren Überblick über den Zusammenhang von Dezimalzahlen und Hexadezimalzahlen.

	Stellenwert
	4 096	256	16	1
0				0
1				1
2				2
3				3
…
10				A
11				B
12				C
13				D
14				E
15				F
16			1	0
17			1	1
18			1	2
19			1	3
…
30			1	E
31			1	F
32			2	0
33			2	1
34			2	2
…
48			3	0
…
63			3	F
64			4	0
65			4	1
…
256		1	0	0
257		1	0	1
…
4094		F	F	E
4095		F	F	F
4096	1	0	0	0
4097	1	0	0	1
…

Zur Geschichte der Hexadezimalzahlen

Das einzige Volk, das Hexadezimalzahlen in der Geschichte verwendete, waren die Chinesen ab ca. 200 v. Chr. Sie nutzten Hexadezimalzahlen für ihr damaliges Gewichtssystem (1 jīn 斤 = 16 liǎng 兩).

Zum Berechnen der Gewichte entwickelten die Chinesen einen Abakus, der „Suanpan“ genannt wurde. Er konnte Dezimalzahlen und Hexadezimalzahlen darstellen. Im 14. Jahrhundert übernahmen die Japaner den „Suanpan“-Abakus. Er wurde von China und Japan bis in die späten 1930er Jahre eingesetzt.

Abbildung 1

Hexadezimalzahlen wurden weltweit erst mit der Einführung von Computern (und der Nutzung von Binärzahlen) berühmt.

Im Jahr 1956 setzte man erstmalig beim Computer „Bendix G-15“ Hexadezimalzahlen ein und verwendete 0 - 9 und u - z.

Das moderne Hexadezimalsystem wurde 1963 vom Unternehmen IBM auf dem Gebiet der Datenverarbeitung als Standard eingeführt. Man entschied sich, die ersten sechs Buchstaben des Alphabets A bis F zu verwenden, um die Werte 10 bis 15 darzustellen.

Die Ziffern A bis F setzen sich schließlich weltweit durch.

Einsatz von Hexadezimalzahlen beim Computer

Doch weshalb wurden ausgerechnet Hexadezimalzahlen für Computer verwendet?

Die größtmögliche Zahl, die eine 4-Bit-Binärzahl darstellen kann, ist 15 dezimal (1111₂ = 15₁₀). Dies ist der gleiche Wert, den eine einzelne Hexadezimalzahl mit F wiedergeben kann (1111₂ = F₁₆).

Wenn wir eine 8-Bit-Binärzahl nehmen, zum Beispiel 1111 0000₂ (= 240₁₀), so lässt sich diese mit nur zwei Ziffern einer Hexadezimalzahl darstellen: F0₁₆.

Vergleichen wir die Unterschiede zwischen in Vierer-Sätzen gruppierten Binärzahlen und Hexadezimalzahlen:

Binär	Hexadezimal	Dezimal
0000 0000 1111	0 0 F	15
0000 1111 0000	0 F 0	240
1111 0000 0000	F 0 0	3840
1111 0000 1111	F 0 F	3855
1111 1111 0000	F F 0	4080
1111 1111 1111	F F F	4095

Wie wir sehen, lässt sich eine 12-stellige Binärzahl wie 1111 1111 1111 mit einer nur 3-stelligen Hexadezimalzahl FFF ausdrücken.

Vorteile von Hexadezimalzahlen

• Programmierer verwenden Hexadezimalzahlen, weil ihre Werte kürzer zu schreiben sind als bei einer dezimalen Darstellung. Sie sind wesentlich kürzer als bei einer binären Darstellung.
• Mit dem Hexadezimalsystem können Daten mit weniger Zeichen festgehalten, also komprimiert werden.
• Hexadezimalzahlen werden insbesondere als Farbcode (HTML/CSS) verwendet, um eine bestimmte Farbe auszudrücken. Zum Beispiel steht FF0000 für Rot, 00FF00 für Grün und 0000FF für Blau.
• Hexadezimalzahlen machen es möglich, riesige Datenströme in einem Computer besser zu verstehen, indem lediglich die Hexadezimal-Ausgabe betrachtet wird, statt der Binär-Ausgabe.
• Hexadezimalzahlen lassen sich sehr schnell in Binärzahlen umrechnen (blockweise).
  Als Beispiel: FAD7 ist als Binärzahl 1111 1010 1101 0111, da F=1111, A=1010, D=1101, 7=0111.