Wir haben nunmehr folgende Zahlensysteme kennengelernt:
- Dezimalzahlen mit den 10 Ziffern: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9
- Binärzahlen mit den 2 Ziffern: 0, 1
- Hexadezimalzahlen mit den 16 Ziffern: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F
Neben diesen drei Zahlensystemen werden häufig auch die Oktalzahlen behandelt:
- Oktalzahlen mit den 8 Ziffern: 0, 1, 2, 3, 4, 5, 6, 7
Stellen wir diese Zahlensystem gegenüber:
| Dezimalzahlen | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| Binärzahlen | 0 | 1 | 10 | 11 | 100 | 101 | 110 | 111 | 1000 | 1001 | 1010 | 1011 | 1100 | 1101 | 1110 | 1111 | 10000 | 10001 |
| Hexadezimalsystem | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F | 10 | 11 |
| Oktalzahlen | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 20 | 21 |
Die fettgedruckten Zahlen zeigen an, dass es zu einem Übertrag auf die nächste Stelle kommt.
Gegenüberstellung (horizontal)
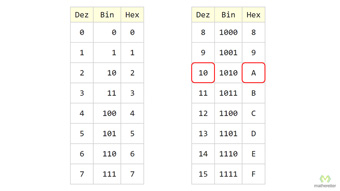
Hier noch eine weitere Gegenüberstellung, wo die Binärzahlen stets mit 4 Stellen wiedergegeben sind.
| Dez | Bin | Hex |
|---|---|---|
| 0 | 0000 | 0 |
| 1 | 0001 | 1 |
| 2 | 0010 | 2 |
| 3 | 0011 | 3 |
| 4 | 0100 | 4 |
| 5 | 0101 | 5 |
| 6 | 0110 | 6 |
| 7 | 0111 | 7 |
| Dez | Bin | Hex |
|---|---|---|
| 8 | 1000 | 8 |
| 9 | 1001 | 9 |
| 10 | 1010 | A |
| 11 | 1011 | B |
| 12 | 1100 | C |
| 13 | 1101 | D |
| 14 | 1110 | E |
| 15 | 1111 | F |
Vorteile und Nachteile
Haben wir eine sehr große Zahl wie zum Beispiel 579862 (dezimal), dann ergibt sich folgende Darstellung je nach Zahlensystem:
- Dezimal: 579862
- Binär: 10001101100100010110
- Hexadezimal: 8D916
- Oktal: 2154426
Wir erkennen sofort, dass wir mit den Hexadezimalzahlen weniger Ziffern benötigen, um eine große Zahl darzustellen. Gleichfalls sehen wir, dass die Binärzahl sehr lang wird, was einen Nachteil bedeutet (mehr Schreibarbeit und Rechenarbeit).
Beispielsweise werden Farben am Computer mit Hexadezimalzahlen ausgedrückt. Also von #000000 (schwarz) bis #FFFFFF (weiß). Es sind somit 16 777 215 verschiedene Farben möglich, wobei im Hexadezimalen nur 6 Ziffern benötigt werden.
Ein Vorteil von Binärzahlen ist, dass sie nur aus 2 Ziffern bestehen. Es ist damit die minimalste Art, Daten zu speichern. Hätten wir nur 1 Zeichen, so wäre es ja immer die gleiche Ziffer und wir könnten keinen Unterschied herbeiführen (000000…).
Zudem beruhen elektrische Geräte wie Computer und Smartphone auf An-Aus-Zuständen (siehe Transistor), die sich direkt binär mit 0 und 1 ausdrücken lassen.
Ein wesentlicher Nachteil von Binärzahlen und Hexadezimalzahlen ist, dass sie schwierig zu lesen sind. Sind sind ungewohnt im Vergleich zu den uns bekannten Dezimalzahlen.