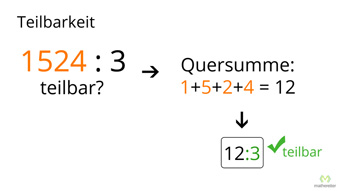
Eine Zahl ist durch 3 teilbar, wenn ihre Quersumme durch 3 teilbar ist. Die Quersumme ist die Summe aller Ziffern der Zahl.
Beispiele
Die Probe ist korrekt, wenn bei der Division eine ganze Zahl herauskommt. Die Zahl ist dann durch die genannte Zahl teilbar.
- 12 Probe mit (1+2) : 3 = 3:3 = 1 ✓
- 243 Probe mit (2+4+3) : 3 = 9:3 = 3 ✓
- 1 524 Probe mit (1+5+2+4) : 3 = 12:3 = 4 ✓
- 3 093 Probe mit (3+0+9+3) : 3 = 15:3 = 5 ✓
Gegenbeispiele
Die Probe ist nicht korrekt, wenn bei der Division ein Rest übrig bleibt (bzw. sich eine Kommazahl ergibt). Die Zahl ist dann durch die genannte Zahl nicht teilbar.
- 19 Probe mit (1+9) : 3 = 10:3 = 3 Rest 1 ✗ bzw. (1+9) : 3 = 10:3 = 3,33… ✗
- 38 Probe mit (3+8) : 3 = 11:3 = 3 Rest 2 ✗ bzw. (3+8) : 3 = 11:3 = 3,66… ✗
- 275 Probe mit (2+7+5) : 3 = 14:3 = 4 Rest 2 ✗ bzw. (2+7+5) : 3 = 14:3 = 4,66… ✗
Mehrfache Anwendung der Quersumme
Es sei erwähnt, dass man die Quersumme auch mehrfach anwenden kann, um die Teilbarkeit durch 3 zu testen.
Als Beispiel:
Ist 99 995 659 695 659 916 durch 3 teilbar?
Zuerst bilden wir die Quersumme: 9+9+9+9+5+6+5+9+6+9+5+6+5+9+9+1+6 = 117
Nun können wir die 117 auf Teilbarkeit durch 3 prüfen:
Quersumme von 117 ist 1+1+7 = 9
9 ist durch 3 teilbar, damit ist auch 117 durch 3 teilbar.
Und damit ist auch 99 995 659 695 659 916 durch 3 teilbar.