Eines der wichtigsten Gebiete der Mathematik befasst sich mit der Analyse von Graphen, bei denen wichtige Informationen mit Hilfe der Differentialrechnung bestimmt werden.
Wir hatten uns bereits im vorangegangenen Kapitel (grafisches Ableiten) einen Überblick verschafft, was die erste Ableitung beschreibt. Wir haben es bei der ersten Ableitung mit der Steigung zu tun, die wir uns aber nicht mehr graphisch herleiten wollen, sondern errechnen. Das spart nicht nur Zeit, sondern ist auch deutlich genauer.
Um uns nochmals an den Begriff der Steigung zu gewöhnen, schauen wir uns ein Beispiel an. Das Beispiel soll eine Gerade sein, an der sich der Begriff am Einfachsten erklärt und deshalb auch im Weiteren eine wichtige Rolle spielt.

Wie wir uns erinnern können, bestimmen wir die Steigung einer Geraden, in dem wir zwei beliebige Punkte auf der Geraden wählen (P1(x1|y1) und P2(x2|y2)) und dann ein Steigungsdreieck basteln. Die Steigung ergibt sich dann aus dem Quotienten \( m = \frac{y_2 - y_1}{x_2 - x_1} = \frac{\Delta y}{\Delta x} \)
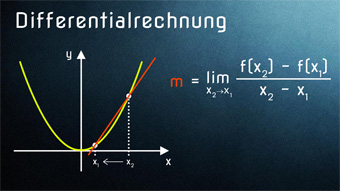
Da die Steigung einer Geraden in jedem Punkt dieselbe ist, ist dieses Vorgehen kein Problem. Doch bereits bei einer Parabel funktioniert diese Herangehensweise nicht mehr. Wählen wir zwei Punkte auf einer Parabel, so sieht man bereits an einem Graphen, dass sich die Steigungen unterscheiden.

Und doch kann man die Gerade als Hilfsmittel verwenden, um eine Steigung in einem Punkt einer Parabel anzunähern. Das schauen wir uns mal genauer an.