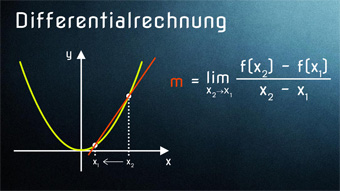
Nachdem wir nun den Differentialquotienten kennengelernt haben und wissen, wie wir die Steigung an einem Punkt berechnen können, wollen wir das Verfahren etwas verallgemeinern und eine Ableitungsfunktion erstellen.
Diese stellen wir mittels der h-Methode auf. Wir wählen hierzu h = x2 - x1. Damit können wir x2 ausdrücken als x2 = x1 + h. Das h geht dabei gegen 0, denn die Differenz der beiden Stellen soll ja ebenfalls 0 sein. Es gilt mit obiger Bedingung f(x2) = f(x1 + h), welches wir nun in den Differentialquotienten einsetzen.
\( m = \lim \limits_{x_2 \to x_1} \frac{f(x_2) - f(x_1)}{x_2 - x_1} = \lim \limits_{h \to 0} \frac{f(x_1 + h) - f(x_1)}{(x_1+h) - x_1} = \lim \limits_{h \to 0} \frac{f(x_1 + h) - f(x_1)}{h} \)
Da wir uns nur noch eine Stelle anschauen, können wir auch allgemeiner schreiben x1 = x.
\( m = \lim \limits_{h \to 0} \frac{f(x + h) - f(x)}{h} \)
Mit dieser allgemeinen Schreibweise können wir nun jede beliebige Stelle direkt anschauen und haben mittels der h-Methode eine Ableitungsfunktion aufgestellt. Um das zu Verschaulichen, schauen wir uns Beispiel 1 nochmals mit der h-Methode an.
Beispiel
Wir hatten ja die Funktion f(x) = x² an der Stelle x = 3 untersuchen wollen.
\( m = \lim \limits_{h \to 0} \frac{f(x + h) - f(x)}{h} = \lim \limits_{h \to 0} \frac{(x+h)^2 - x^2}{h} = \lim \limits_{h \to 0} \frac{x^2 + 2xh + h^2 - x^2}{h} = \lim \limits_{h \to 0}\frac{2xh + h^2}{h} = \lim \limits_{h \to 0} \frac{h(2x+h)}{h} = \lim \limits_{h \to 0} 2x + h = 2·x \)
Wenn wir nun die Stelle x = 3 untersuchen wollen, rechnen wir m = 2·x = 2·3 = 6. Wie wir anhand von Beispiel 1 überprüfen können, ist das Ergebnis korrekt. Da wir aber allgemeiner gerechnet haben, ist die Bezeichnung m unpraktisch, die wir bisher für den Wert einer Steigung gewählt haben. Die Ableitungsfunktion selbst wird mit f’(x) gekennzeichnet. Wir setzen also an das f ein kleines Apostroph.
\( f'(x) = \lim \limits_{h \to 0} \frac{f(x_1 + h) - f(x_1)}{h} \)
Mit dieser Information können wir ganz allgemein die Ableitungsfunktion des Graphen f(x) = x² mit f’(x) = 2·x angeben. Zur Analyse der Steigung an einer beliebigen Stelle, besteht nun der einzige Aufwand darin, den x-Wert in die Ableitungsfunktion einzusetzen.
Wenn wir die Steigung an der Stelle x = 5 bei f(x) = x² wissen möchten, rechnen wir:
f’(x) = 2·x
f’(5) = 2·5 = 10
Die Steigung (der Tangente) an der Stelle x = 5 beträgt also 10.