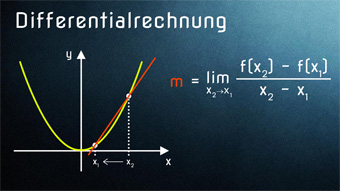
Wie gerade besprochen, wollen wir auf die Geraden zurückgreifen - bei denen wir kein Problem haben, die Steigung zu bestimmen - um eine Aussage über die Steigung einer Parabel oder anderen Funktionen treffen zu können. Dies kann nur als grobe Näherung betrachtet werden, bringt uns aber dem Ziel näher, die tatsächliche Ableitungsfunktion bestimmen zu können.
Um nun die Steigung einer Parabel in einem Bereich bestimmen zu können, verwenden wir das Hilfsmittel einer Sekante. Die Sekante ist ja eine Gerade, welche einen Graphen in zwei Punkten schneidet.

Wie wir im obigen Graphen erkennen können, verläuft die Sekante sehr nahe an dem Graphen von f (in einem bestimmten Bereich) und somit kann zumindest näherungsweise eine Aussage über die Steigungen zwischen P1 und P2 getroffen werden, indem man sich auf die Werte der Geraden beruft.
Demnach lässt sich der Differenzenquotient wie gewohnt ausdrücken über
\( m = \frac{y_2 - y_1}{x_2 - x_1} = \frac{\Delta y}{\Delta x} \)
Da wir es jedoch nicht mit beliebigen Punkten D zu tun haben, sondern diese auf dem Graphen der Funktion liegen und die y-Werte einem x-Wert zugeordnet sind, ist die üblichere Schreibweise:
\( m = \frac{f(x_2) - f(x_1)}{x_2 - x_1} = \frac{\Delta y}{\Delta x} \)
Statt einer gewöhnlichen Geradensteigung haben wir nun die Steigung einer Sekante bestimmt. Der Wert der Angabe über die Steigung der eigentlichen Funktion wird dabei umso genauer je geringer der Abstand zwischen den x-Werten ist. Beispiel:
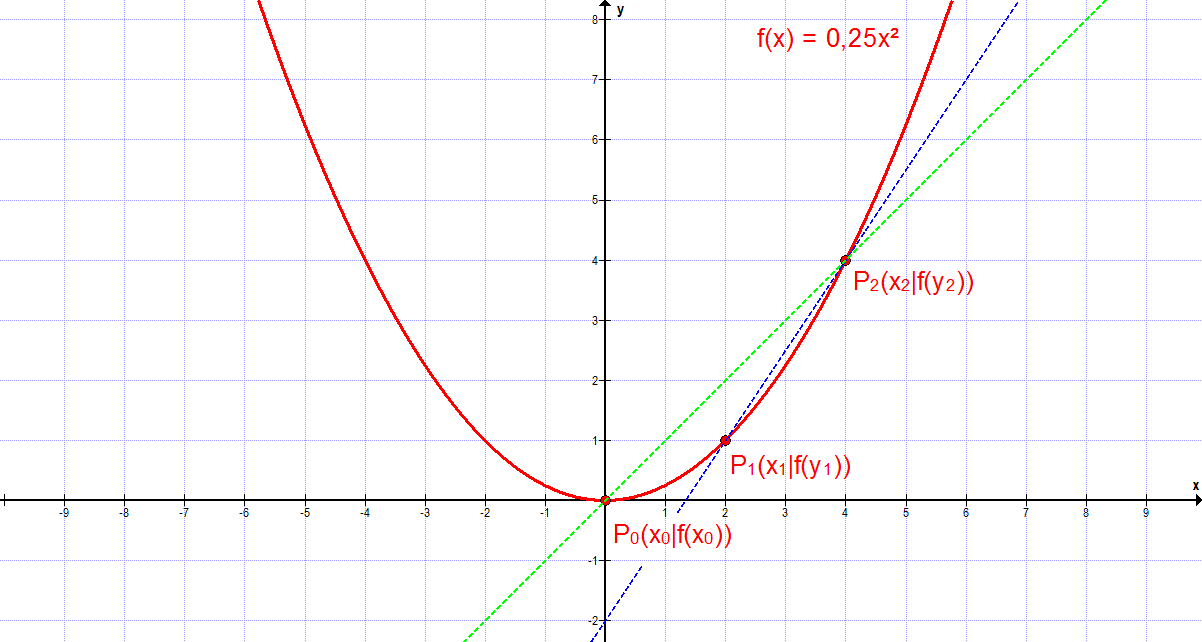
Wählt man die beiden Punkte P0 und P2 (x-Werte haben einen Abstand von Δx = 4), weicht die Sekante stark von der eigentlichen Funktion f ab. Wählt man hingegen die beiden Punkte P1 und P2 (x-Werte haben einen Abstand von Δx = 2), ist die Angabe der Steigung hinreichend genau.
Dieser Gedanke führt uns auch direkt zum nächsten Kapitel, dem Differentialquotienten.