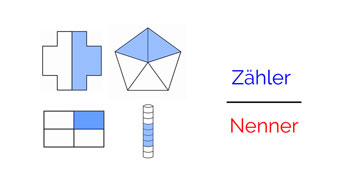
Brüche lassen sich als Anteile von einem Ganzen verstehen. Das Ganze teilt man in mehrere Teile. Im Folgenden ein paar Beispiele hierzu, bei denen wir die Bruchteile zeichnerisch darstellen. Dabei ist die Frage immer: In wie viele Teile wurde das Ganze geteilt? Wie heißt der gefärbte Anteil?
Beispiel 1: Kreis
Der ganze Kreis wurde in 4 Teile geteilt. 1 Teil wurde markiert.
Wir schreiben als Bruch: \( \large{\frac{\textcolor{#00F}{1}}{\textcolor{#F00}{4}}} \)
Wir sprechen „1 von 4“ bzw. „ein Viertel“.
Beispiel 2: Kreis
Der ganze Kreis wurde in 6 Teile geteilt. 1 Teil wurde markiert.
Wir schreiben als Bruch: \( \large{\frac{\textcolor{#00F}{1}}{\textcolor{#F00}{6}}} \)
Beispiel 3: Kreis
Der ganze Kreis wurde in 8 Teile geteilt. 3 Teile wurden markiert.
Wir schreiben als Bruch: \( \large{\frac{\textcolor{#00F}{3}}{\textcolor{#F00}{8}}} \)
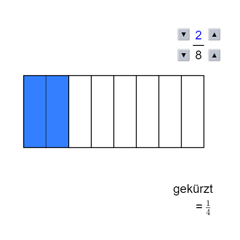
Beispiel 4: Rechteck
Das Rechteck wurde in 4 Teile geteilt. 1 Teil wurde markiert.
Wir schreiben als Bruch: \( \large{\frac{\textcolor{#00F}{1}}{\textcolor{#F00}{4}}} \)
Beispiel 5: Figur
Die Figur wurde in 2 Teile geteilt. 1 Teil wurde markiert.
Wir schreiben als Bruch: \( \large{\frac{\textcolor{#00F}{1}}{\textcolor{#F00}{2}}} \)
Beispiel 6: Rechteck/Streifen
Der Streifen wurde in 7 Teile geteilt. 1 Teil wurde markiert.
Wir schreiben als Bruch: \( \large{\frac{\textcolor{#00F}{1}}{\textcolor{#F00}{7}}} \)
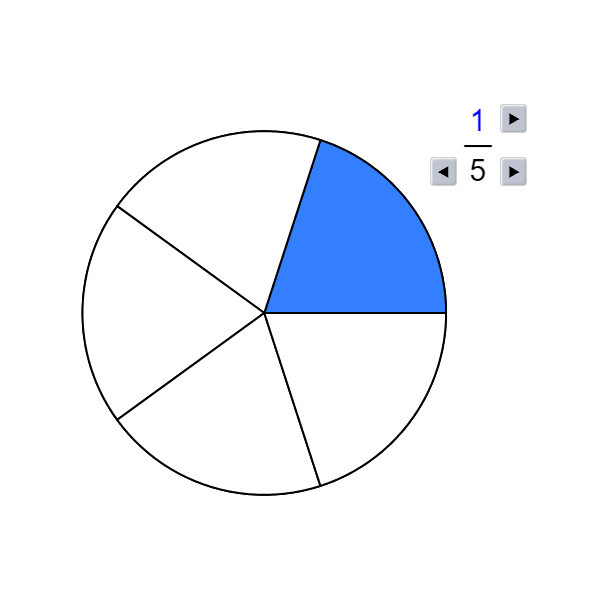
Beispiel 7: Fünfeck
Das Fünfeck wurde in 5 Teile geteilt. 2 Teile wurden markiert.
Wir schreiben als Bruch: \( \large{\frac{\textcolor{#00F}{2}}{\textcolor{#F00}{5}}} \)
Beispiel 8: Zylinder
Der Zylinder wurde in 9 Teile geteilt. 4 Teile wurden markiert.
Wir schreiben als Bruch: \( \large{\frac{\textcolor{#00F}{4}}{\textcolor{#F00}{9}}} \)
Beispiel 9: Quader
Der Quader wurde in 8 Teile geteilt. 1 Teil wurde markiert.
Wir schreiben als Bruch: \( \large{\frac{\textcolor{#00F}{1}}{\textcolor{#F00}{8}}} \)