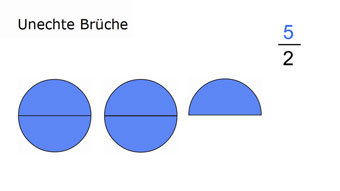
Wir sprechen von „unechten Brüchen“, wenn der Zähler des Bruches größer ist als der Nenner.
Beispiel: \( \textcolor{#00F}{\frac{5}{2}} \)
Weitere Beispiele unechter Brüche: \( \frac{7}{3}, \frac{6}{5}, \frac{25}{7}, \frac{110}{3}, \frac{99}{97} \)
Dividieren wir Zähler und Nenner, so erhalten wir den Dezimalwert des Bruches.
Für die vorgenannten Beispiel ergibt sich:
\( \frac{5}{2} \textcolor{#55F}{ = 2,5 } \quad \frac{7}{3} \textcolor{#55F}{ = 2,\overline{3} } \quad \frac{6}{5} \textcolor{#55F}{ = 1,2 } \quad \allowbreak \frac{25}{7} \textcolor{#55F}{ ≈ 3,57 } \quad \frac{110}{3} \textcolor{#55F}{ = 36,\overline{6} } \quad \frac{99}{97} \textcolor{#55F}{ ≈ 1,02 } \)
Anhand der Dezimalwerte können wir die Brüche in ihrer Größe miteinander vergleichen und sortieren:
\( \frac{99}{97} \textcolor{#55F}{ ≈ 1,02 } \quad \frac{6}{5} \textcolor{#55F}{ = 1,2 } \quad \frac{7}{3} \textcolor{#55F}{ = 2,\overline{3} } \quad \frac{5}{2} \textcolor{#55F}{ = 2,5 } \quad \allowbreak \frac{25}{7} \textcolor{#55F}{ ≈ 3,57 } \quad \frac{110}{3} \textcolor{#55F}{ = 36,\overline{6} } \)
Unechter Bruch (grafisch)
Es sei angemerkt, dass sich unechte Brüche nicht an einem Kreis einzeichnen lassen, da ihr Wert größer als 1 ist. Wir müssen hierzu mehrere Kreise verwenden.
Der unechte Bruch \( \frac{7}{2} \) lässt sich mit 7 Kreishälften darstellen:
Wir haben 7 mal \( \frac{1}{2} \) gezeichnet.
Unechte Brüche vergleichen
Wir hatten bereits gelernt, wie man gleichnamige Brüche sowie ungleichnamige Brüche vergleicht. Das dort Gesagte gilt für die unechten Brüche ebenfalls:
Gleichnamige unechte Brüche vergleichen
Da wir bereits gleiche Nenner vorliegen haben, können wir direkt die Zähler miteinander vergleichen. Ist der Zähler größer, so ist auch der Bruch größer.
Beispiel: \( \frac{7}{2} > \frac{5}{2} \)
Ungleichnamige unechte Brüche vergleichen
Hier müssen wir durch Erweitern oder Kürzen den gleichen Nenner bei beiden Brüchen schaffen. Erst dann lassen sich die Brüche vergleichen.
Wollen wir beispielsweise \( \frac{12}{7} \) mit \( \frac{15}{8} \) vergleichen, so schaffen wir zuerst den gemeinsamen Nenner mit 7·8 = 56, indem wir jeden Bruch entsprechend erweitern:
\( \frac{ 12 \textcolor{#00F}{·8} }{7 \textcolor{#00F}{·8} } = \frac{96}{56} \) sowie \( \frac{ 15 \textcolor{#00F}{·7} }{8 \textcolor{#00F}{·7} } = \frac{105}{56} \)
Dann können wir direkt die Zähler vergleichen: 96 ist kleiner als 105, damit gilt:
\( \frac{96}{56} < \frac{105}{56} \) und \( \frac{12}{7} < \frac{15}{8} \)
Dezimalwerte von Brüchen
Nachfolgend noch der Hinweis, wie man am Dezimalwert des Bruches erkennt, um welchen Typ von Bruch es sich handelt.
-
Ist der Dezimalwert des Bruches zwischen 0 und 1,
so handelt es sich um einen echten Bruch.
Beispiel: \( \frac{1}{4} = 0,25 \) und 0,25 liegt zwischen 0 und 1. Wir schreiben: 0 < 0,25 < 1. -
Ist der Dezimalwert des Bruches eine ganze Zahl, so ist es ein Scheinbruch.
Beispiel 1: \( \frac{3}{3} = 1 \) und 1 ist eine ganze Zahl.
Beispiel 2: \( \frac{15}{3} = 5 \) und 5 ist eine ganze Zahl. -
Ist der Dezimalwert des Bruches größer als 1, so ist es ein unechter Bruch.
Beispiel: \( \frac{10}{4} = 2,5 \) und 2,5 ist größer als 1. Wir schreiben: 2,5 > 1.