Brüche - Einführung

Brüche werden sehr oft in der Mathematik benötigt. Sie sind ein wichtiges Werkzeug zum Rechnen.

Auch im Alltag lassen sich Brüche finden. So sagen wir zum Beispiel „ein halbes Brot“ oder „eine halbe Stunde“, was beides den Bruch \( \dfrac{1}{2} \) darstellt.

Weitere Beispiele aus dem Alltag wären:

• Eine halbe Torte: \( \frac{1}{2} \) („ein halb“).
• Die Apfelschorle besteht zu \( \frac{4}{5} \) („vier fünftel“) aus Apfelsaft.
• Eine Dreiviertelstunde ist vorbei: \( \frac{3}{4} \) („drei viertel“) Stunde.

Brüche anschaulich

Wir können uns einen Bruch wie \( \dfrac{1}{4} \) auch grafisch vorstellen.

Hierzu teilen wir ein Objekt in 4 gleich große Stücke auf und markieren anschließend 1 davon.

Zum Beispiel können wir eine Pizza in 4 gleich große Stücke schneiden und markieren dann 1 Stück davon:

„1 von 4“ Stück Pizza ist als Bruch \( \dfrac{ \color{#00F}{1} }{ \color{#F00}{4} } \).

Nehmen wir uns die genannten Beispiele aus dem Alltag und zeigen auf, wie hier aufgeteilt wurde. Hier müssen wir jeweils das gegebene Objekt in die genannte Anzahl an gleich großen Teilen zerlegen und die gegebene Anzahl auswählen.

• Eine halbe Torte.
  \( \dfrac{ \color{#00F}{1} }{2} \) → Zerlege das Objekt (die Torte) in 2 gleich große Teile und markiere 1 davon.
• Die Apfelschorle besteht zu \( \frac{4}{5} \) aus Apfelsaft.
  \( \dfrac{ \color{#00F}{4} }{5} \) → Zerlege das Objekt (die Apfelschorle) in 5 gleich große Teile und markiere 4 davon.
• Eine Dreiviertelstunde.
  \( \dfrac{ \color{#00F}{3} }{4} \) → Zerlege das Objekt (die Stunde) in 4 gleich große Teile und markiere 3 davon.

Was ist ein Bruch?

Wir können einen Bruch wie folgt beschreiben:

Dabei legen wir fest, welches Objekt als Ganzes gilt und in wie viele Teile es zerlegt werden soll.

Eine Pizza kann halbiert werden, dann ist eine Hälfte der Pizza \( \dfrac{1}{2} \) (1 von 2 Teilen).

Eine Pizza kann geviertelt werden, dann ist ein Viertel der Pizza \( \dfrac{1}{4} \) (1 von 4 Teilen).

Eine Pizza kann geachtelt werden, dann ist ein Achtel der Pizza \( \dfrac{1}{8} \) (1 von 8 Teilen).

Namen von Brüchen

Brüche spricht man wie folgt aus:

• \( \dfrac{1}{2} \) → „ein Halb“
• \( \dfrac{1}{3} \) → „ein Drittel“
• \( \dfrac{1}{4} \) → „ein Viertel“
• \( \dfrac{1}{5} \) → „ein Fünftel“
• \( \dfrac{1}{6} \) → „ein Sechstel“
• \( \dfrac{1}{7} \) → „ein Siebentel“
• \( \dfrac{1}{8} \) → „ein Achtel“
• \( \dfrac{1}{9} \) → „ein Neuntel“
• \( \dfrac{1}{10} \) → „ein Zehntel“
• und so weiter.

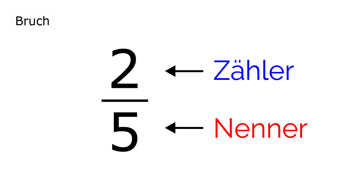
Begriffe: Zähler und Nenner

Es gibt zwei Bezeichnungen beim Bruch:

1. Die Zahl, die oben auf dem Bruchstrich steht, heißt „Zähler“ (sie zählt die gewählten Stücke).

2. Die Zahl, die unter dem Bruchstrich steht, heißt „Nenner“ (sie beschreibt die insgesamt vorhandenen Stücke):

$$ \frac{ \text{Zähler} }{ \text{Nenner} } \rightarrow \text{ Beispiel: } \frac{1}{2}$$

Bei \( \dfrac{ \textcolor{#00F}{1} }{ \textcolor{#F00}{2} } \) bedeutet das:

1 gewähltes Stück („Zähler“)
von insgesamt 2 Stücken („Nenner“).

Bruch als Division und Division als Bruch

Es sei abschließend angemerkt, dass wir jeden Bruch als Division schreiben können. Zum Beispiel:

\( \dfrac{ \color{#00F}{1} }{ \color{#F00}{3} } \) können wir schreiben als 1 : 3.

Dieses Umschreiben ist mit jedem Bruch möglich.

Auch können wir jede Divison als Bruch schreiben.

Nehmen wir als Beispiel 1 : 4. Hier ersetzen wir das Divisionszeichen : mit einem Bruchstrich \( \dfrac{ \phantom{x} }{ \phantom{y} } \) und schreiben danach die 1 oben auf den Bruchstrich und die 4 unten unter den Bruchstrich.

So wird aus 1 : 4 der Bruch \( \dfrac{ \color{#00F}{1} }{ \color{#F00}{4} } \).

Schauen wir uns als nächstes die Brüche am Kreis an.