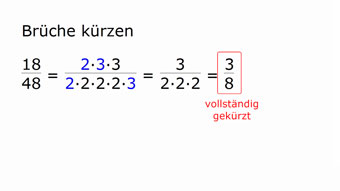
Wir hatten bereits gelernt, wie man Brüche kürzen kann, zum Beispiel:
\( \frac{12}{24} = \frac{12\textcolor{blue}{:2}}{24\textcolor{blue}{:2}} = \frac{6}{12} \)
Hier stellen wir fest, dass sich \( \frac{6}{12} \) nochmals kürzen lässt: \( \frac{6:2}{12:2} = \frac{3}{6} \) und noch ein weiteres Mal gekürzt: \( \frac{3:3}{6:3} = \frac{1}{2} \).
Wir hätten sinnvoller Weise also gleich vollständig kürzen können:
\( \frac{12}{24} = \frac{12 \textcolor{#00F}{:12} }{24 \textcolor{#00F}{:12}} = \frac{1}{2} \)
Spricht man vom „vollständigen Kürzen“, so meint man also immer, dass der Bruch nicht mehr kürzbar ist.
Primfaktorzerlegung zum Kürzen von Brüchen
Wenn wir sehen wollen, wie weit sich ein Bruch kürzen lässt, so können wir uns die Zerlegung in Primfaktoren zur Hilfe nehmen. Hier ist es notwendig, dass wir uns erinnern, was Primzahlen sind.
Wollen wir zum Beispiel den Bruch \( \frac{100}{12} \) vollständig kürzen, so zerlegen wir den Zähler und den Nenner in Primzahlen bzw. Primfaktoren:
\( \frac{100}{12} = \frac{2 · 2 · 5 · 5}{2 · 2 · 3} \)
Im nächsten Schritt können wir die gleichen Faktoren im Zähler und Nenner streichen und das Ergebnis ausrechnen:
\( \frac{2 · 2 · 5 · 5}{2 · 2 · 3} = \frac{ \textcolor{#777}{\cancel{2}} · \textcolor{#777}{\cancel{2}} · 5 · 5}{ \textcolor{#777}{\cancel{2}} · \textcolor{#777}{\cancel{2}} · 3} = \frac{25}{3} \)
Der Bruch ist jetzt vollständig gekürzt.