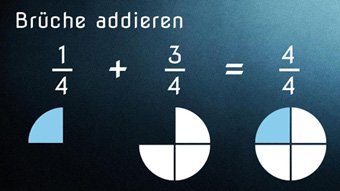
Bei gleichnamigen Brüchen (gleiche Nenner) können wir direkt die Zähler subtrahieren. Der Nenner bleibt auch beim Ergebnis gleich:
$$ \frac{4}{7} - \frac{1}{7} = \frac{4-1}{7} = \frac{3}{7} $$
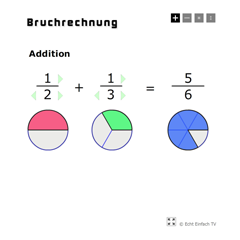
Bei ungleichnamigen Brüchen (ungleiche Nenner) müssen wir zuerst durch Erweitern den gleichen Nenner bilden und können dann subtrahieren:
$$ \frac{3}{7} - \frac{1}{8} = \frac{3 \textcolor{#00F}{·8}}{7\textcolor{#00F}{·8}} - \frac{1\textcolor{#F00}{·7}}{8\textcolor{#F00}{·7}} = \frac{24}{56} - \frac{7}{56} = \frac{24-7}{56} = \frac{17}{56} $$
Allgemein:
Bei der Subtraktion von Brüchen gelten die gleichen Regeln wie bei der Addition von Brüchen, nur dass wir ein Minuszeichen setzen:
$$ \frac{a}{\textcolor{red}{b}} - \frac{c}{\textcolor{blue}{d}} = \frac{a\textcolor{blue}{·d}}{b\textcolor{blue}{·d}} - \frac{c\textcolor{red}{·b}}{d\textcolor{red}{·b}} = \frac{a·d - c·b}{\textcolor{red}{b}·\textcolor{blue}{d}} $$
Subtraktion von Brüchen (grafisch)
Grafisch kann man die Subtraktion zweier Brüche wie folgt darstellen. Hier werden die Flächenstücke voneinander abgezogen: