Grundsätzlich gelten für 3D-Operationen die gleichen Betrachtungen wie für 2D. Auch hier ist die Anwendung der homogenen Koordinaten angebracht, da auch hier die Vereinheitlichung der Operationen mit nur einem Matrix-Komplex ökonomische Vorteile hat. Dennoch: es gibt Unterschiede in der Betrachtung der 2D- und 3D-Transformationen. Die wichtigsten Unterschiede sind:
a) die Rotation in 2D, die sich auf eine Rotation um den Ursprung reduzieren ließ, ist in 3D nunmehr eine zusammengesetzte Operation um die Achsen des dreidimensionalen Raumes und
b) 3D-Objekte sind auf einem 2D-Bildschirm nicht direkt darstellbar.
Orientierung
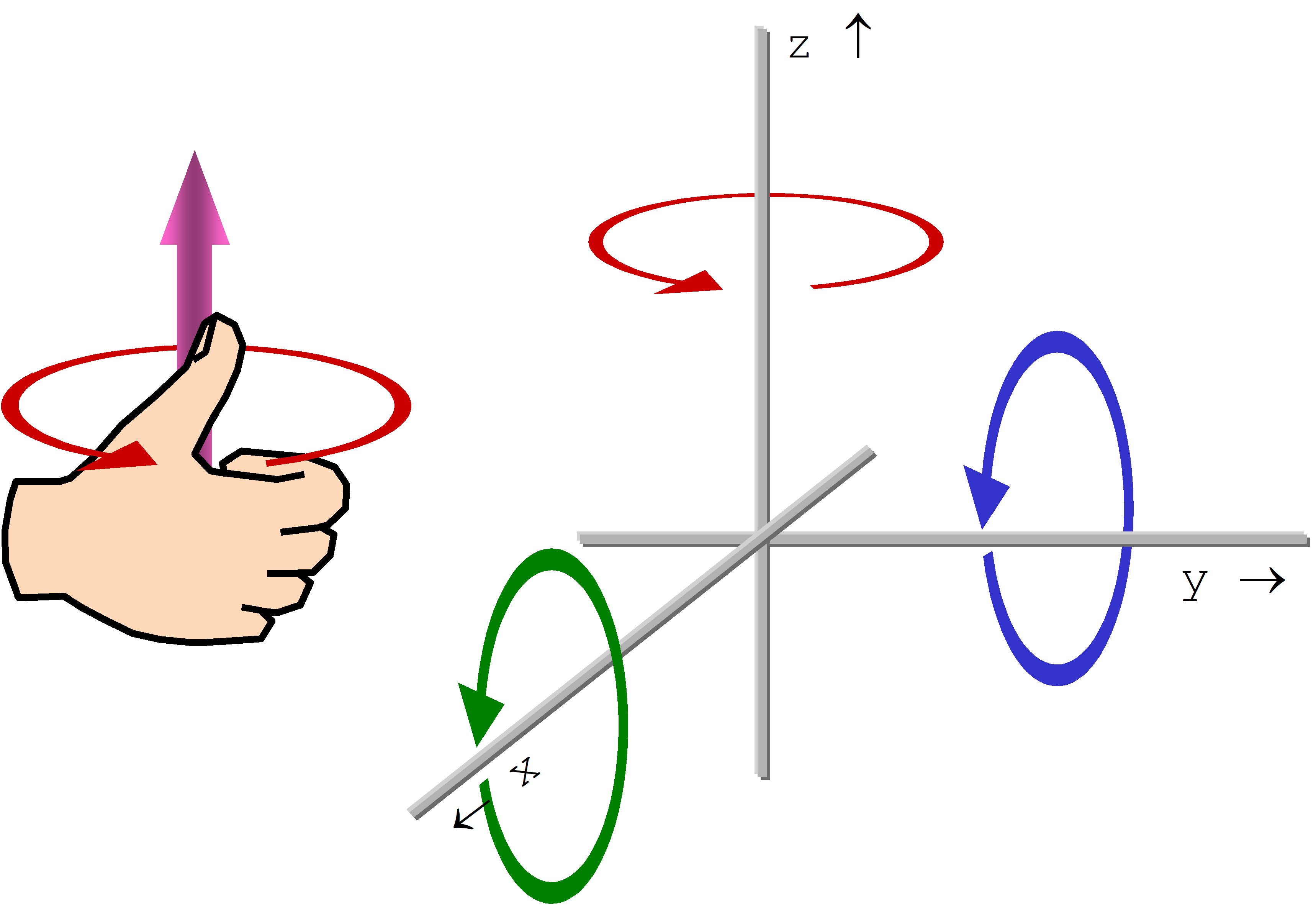
Für die Orientierung im Raum ist es zweckmäßig, mit einem System von Richtungsvorgaben zu arbeiten. Als Gedankenstütze verwende man die Rechte-Hand-Regel:
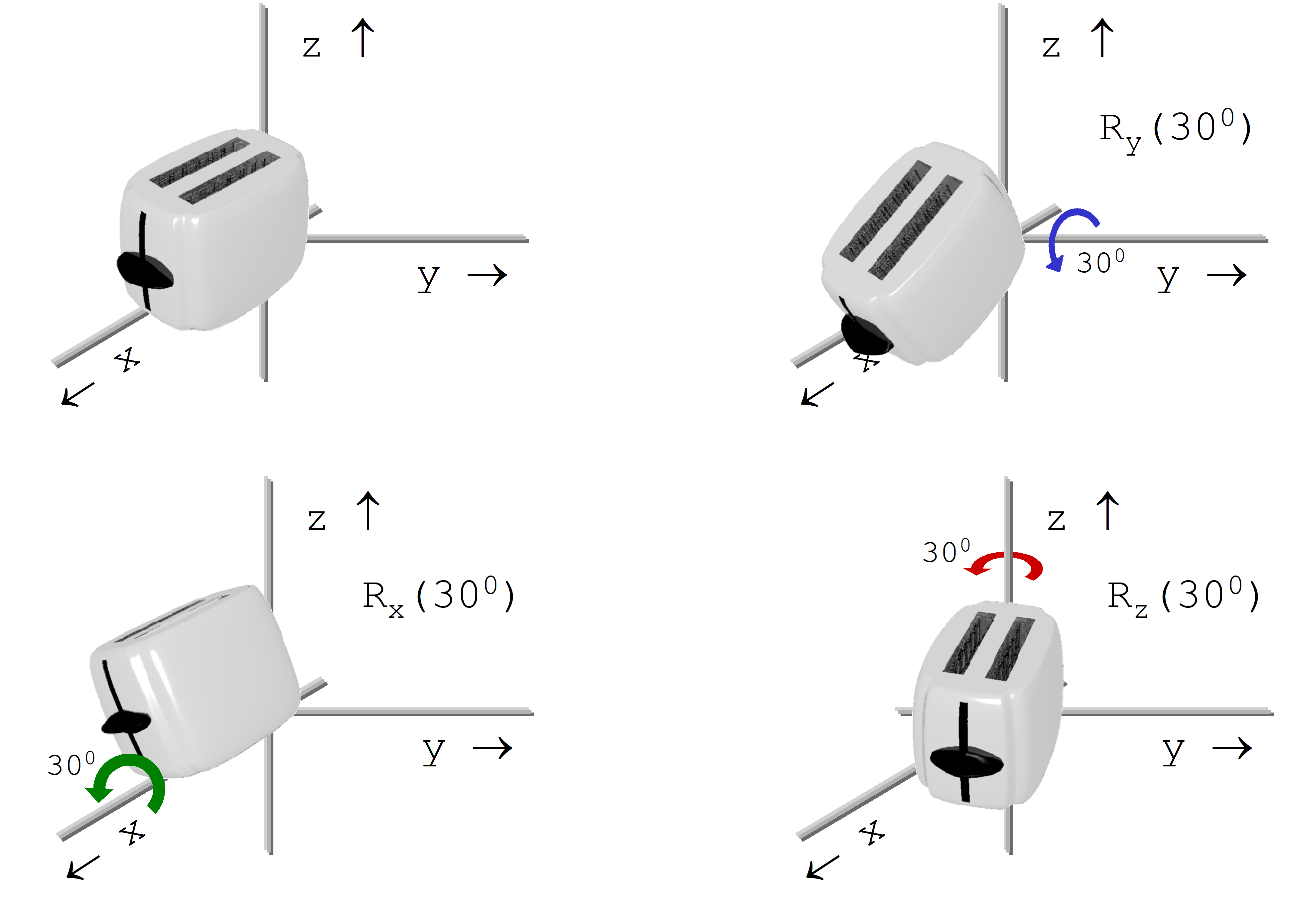
Rotationen um eine der Achsen werden als positiv angesehen, wenn sie den in der folgenden Abbildung gezeigten Orientierungen folgen.
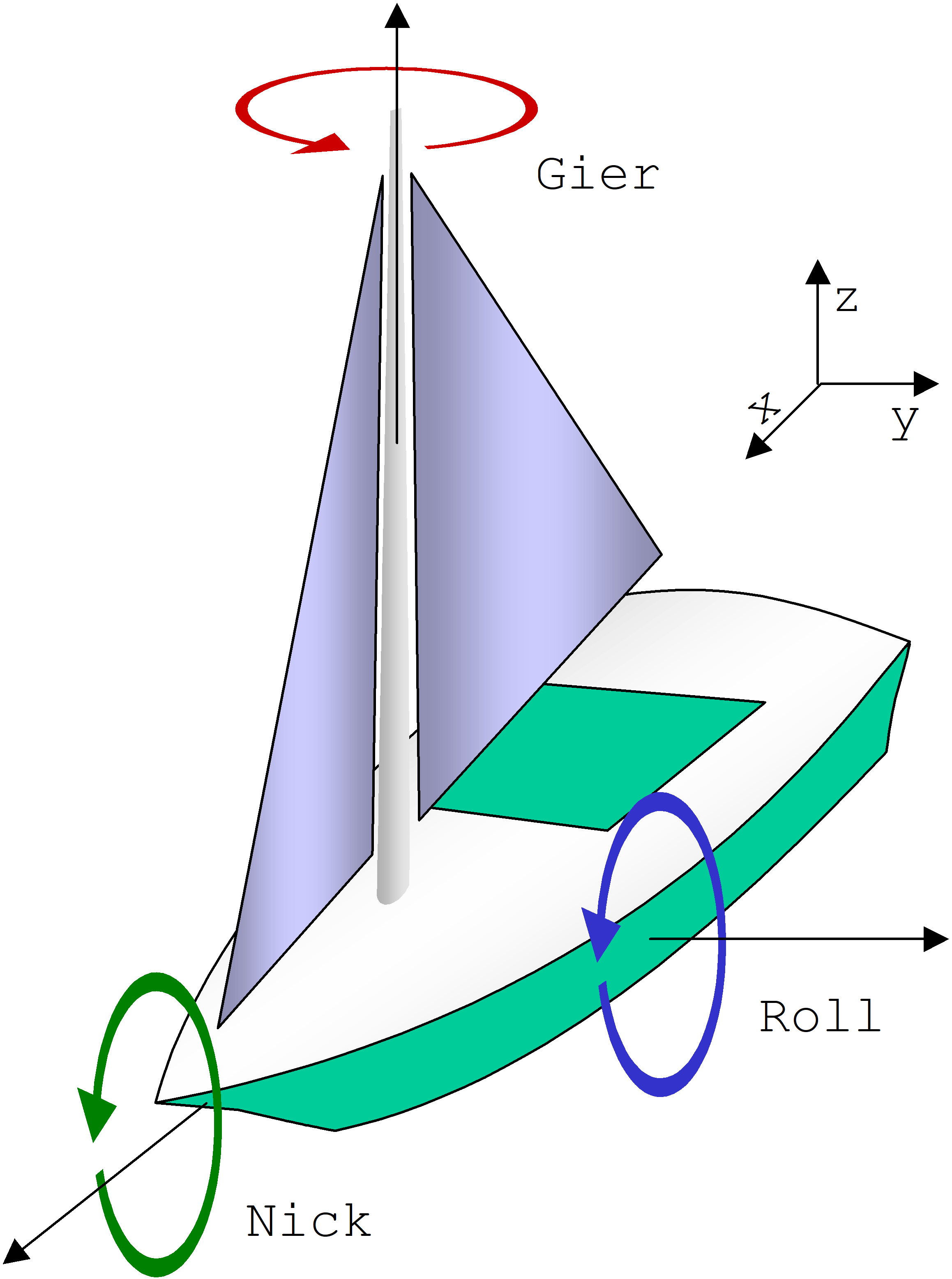
Die verwendeten Bezeichnungen stammen aus der Schifffahrt: Die z-Achse entspricht dabei dem Mast eines Seglers und die x-Achse verläuft parallel zum Schiffsrumpf in Fahrtrichtung. Bezeichnungen sind Gier, Roll und Nick.
Transformationen
Im homogenen Koordinatensystem werden dreidimensionale Objekte durch vierzeilige Spaltenvektoren bzw. Transformationen durch 4x4-Matrizen dargestellt. Analog zu den Transformationen in 2D werden die Transformationen
Translation
\( T = \left( {\begin{array}{cc}1&0&0&{ {t_x} }\\0&1&0&{ {t_y} }\\0&0&1&{ {t_z} }\\0&0&0&1\end{array} } \right) \quad \text{ bzw. } \quad {T^{ - 1} } = \left( {\begin{array}{cc}1&0&0&{ - {t_x} }\\0&1&0&{ - {t_y} }\\0&0&1&{ - {t_z} }\\0&0&0&1\end{array} } \right) \) Gl. 237
Skalierung
\( S = \left( {\begin{array}{cc}{ {s_x} }&0&0&0\\0&{ {s_y} }&0&0\\0&0&{ {s_z} }&0\\0&0&0&1\end{array} } \right) \quad \text{ bzw. } \quad {S^{ - 1} } = \left( {\begin{array}{cc}{\frac{1}{ { {s_x} } } }&0&0&0\\0&{\frac{1}{ { {s_y} } } }&0&0\\0&0&{\frac{1}{ { {s_z} } } }&0\\0&0&0&1\end{array} } \right) \) Gl. 238
Scherung
Die Scherung erfolgt in 3D nicht mehr entlang einer Achse sondern einer Fläche, die durch zwei Achsen aufgespannt wird. Da es drei solche Flächen gibt, sind auch drei elementare Scherungen möglich:
\( S{h_{xy} } = \left( {\begin{array}{cc}1&0&{ {a_x} }&0\\0&1&{ {a_y} }&0\\0&0&1&0\\0&0&0&1\end{array} } \right) \quad S{h_{yz} } = \left( {\begin{array}{cc}1&0&0&0\\{ {a_y} }&1&0&0\\{ {a_z} }&0&1&0\\0&0&0&1\end{array} } \right) \quad S{h_{xz} } = \left( {\begin{array}{cc}1&{ {a_x} }&0&0\\0&1&0&0\\0&{ {a_z} }&1&0\\0&0&0&1\end{array} } \right) \) Gl. 239
Wobei Shxy eine Scherung parallel zur xy-Ebene (Abbildung 24), Shyz eine Scherung parallel zur yz-Ebene und Shxz eine Scherung parallel zur xz-Ebene bedeuten.

Rotation
Auch bei der Rotation haben sich die Verhältnisse verkompliziert. In 3D gibt es ebenfalls drei elementare Rotationen um die einzelnen Achsen des Koordinatensystems:
\( {R_z} = \left( { \begin{array}{cc} {\cos \alpha }&{ -\sin \alpha }&0&0 \\ {\sin \alpha }&{\cos \alpha}&0&0 \\ 0&0&1&0 \\ 0&0&0&1 \end{array} } \right) \) Gl. 240
Die Rotation um die z-Achse entspricht der 2D-Rotation um den Ursprung, in den die z-Achse projiziert vorgestellt werden kann.
\({R_x} = \left( {\begin{array}{cc}1&0&0&0\\0&{\cos \beta }&{ - \sin \beta }&0\\0&{\sin \beta }&{\cos \beta }&0\\0&0&0&1\end{array} } \right)\) Gl. 241
\( {R_y} = \left( {\begin{array}{cc}{\cos \gamma }&0&{\sin \gamma }&0\\0&1&0&0\\{ - \sin \gamma }&0&{\cos \gamma }&0\\0&0&0&1\end{array} } \right) \) Gl. 242
Rz ist die Rotation um den Winkel a um die z-Achse, Rx die Rotation um den Winkel b um die x-Achse und Ry die Rotation um den Winkel g um die y-Achse (Abbildung 25).