Zur Lösung bestimmter Aufgaben ist die Multiplikation von Matrizen erforderlich. Als Beispiel sei genannt:
\(Y = A \cdot B \cdot X = C \cdot X \Rightarrow C = A \cdot B\,?\) Gl. 146
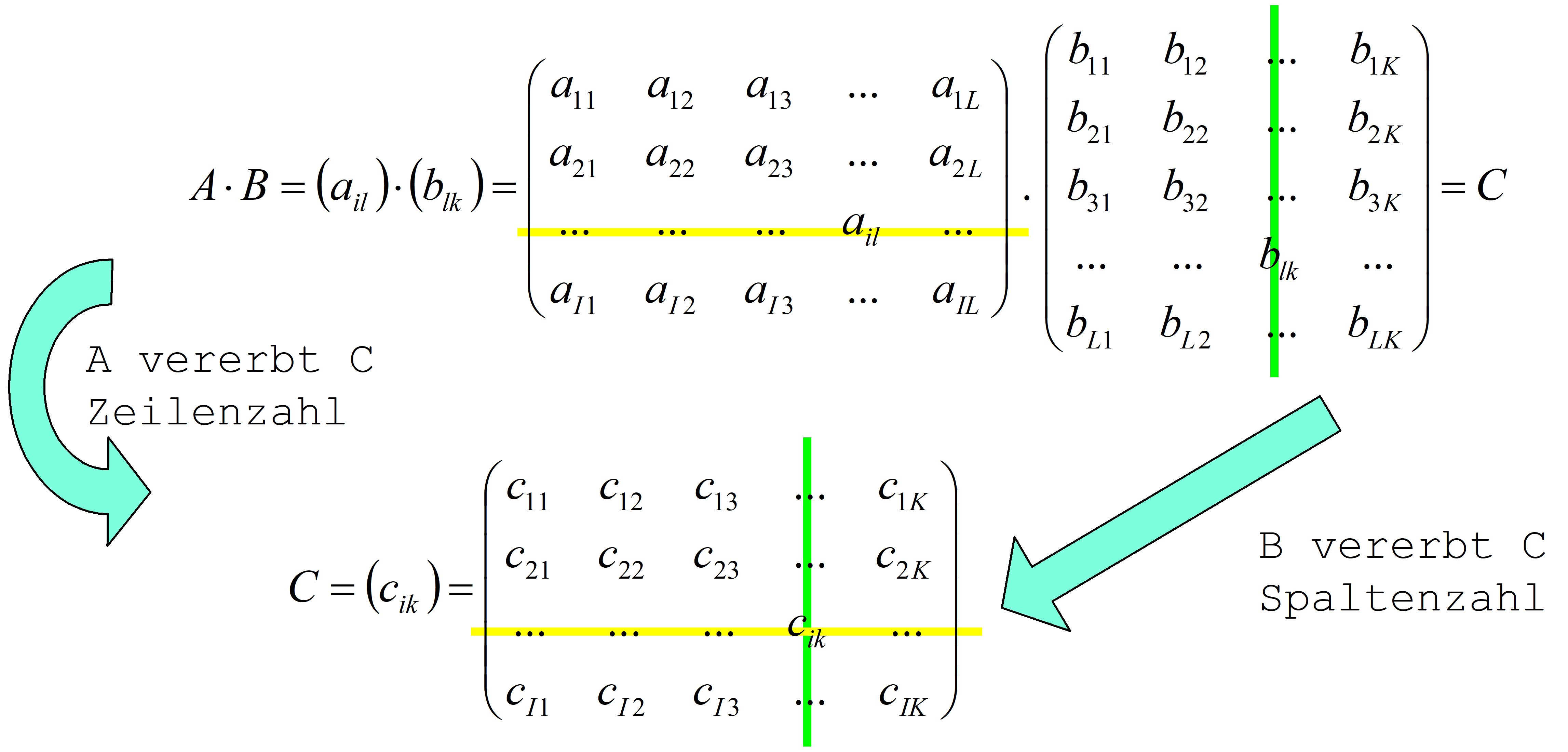
Voraussetzung für die Ausführbarkeit einer Matrizenmultiplikation ist die Übereinstimmung der Spaltenanzahl der linken Matrix (hier AIL) mit der Zeilenanzahl der rechten Matrix (hier BLK).
Stimmen die Spaltenanzahl der linken und die Zeilenanzahl der rechten Matrix nicht überein, sind entsprechend viele Zeilen oder Spalten mit Nullen aufzufüllen. Dies gilt prinzipiell auch für Matrizen, die in keiner Dimension übereinstimmen.
Die Multiplikationsvorschrift für jedes Element der resultierenden Matrix lautet
\({c_{ik} } = \sum\limits_{l = 1}^L { {a_{il} } } \cdot {b_{lk} }\) \(\left\{ \begin{array}{l}i = 1...I\\k = 1...K\end{array} \right.\) Gl. 147
Schematisch wird dabei so vorgegangen, dass alleL Elemente der i-ten Zeile der linken Matrix (A) elementweise mit allen L Elementen der k-ten Spalte der rechten Matrix (B) multipliziert und addiert werden. Dadurch entsteht ein Skalar, der das Element cik des Matrizenproduktes (C) bildet:
Beispiel:
Gesucht ist das Produkt der Matrizen A und B
\( A = \left( {\begin{array}{cc}2&3&{-2}\\4&2&1\\{ - 2}&5&3\end{array} } \right); \qquad B = \left( {\begin{array}{cc}2&3\\{-1}&2\\3&{ - 2}\end{array} } \right) \)
\( A \cdot B = C = \left( {\begin{array}{cc}{\left( {2 \cdot 2 + 3 \cdot \left( { - 1} \right) - 2 \cdot 3} \right)}\\{\left( {4 \cdot 2 + 2 \cdot \left( { - 1} \right) + 1 \cdot 3} \right)}\\{\left( { - 2 \cdot 2 + 5 \cdot \left( { - 1} \right) + 3 \cdot 3} \right)\,\,\,\,}\end{array}\begin{array}{cc}{\left( {2 \cdot 3 + 3 \cdot 2 - 2 \cdot \left( { - 2} \right)} \right)}\\{\left( {4 \cdot 3 + 2 \cdot 2 + 1 \cdot \left( { - 2} \right)} \right)}\\{\left( { - 2 \cdot 3 + 5 \cdot 2 + 3 \cdot \left( { - 2} \right)} \right)}\end{array} } \right) = \left( {\begin{array}{cc}{\left( { - 5} \right)}\\9\\0\end{array}\begin{array}{cc}{16}\\{14}\\{\left( { - 2} \right)}\end{array} } \right) \)
Im Idealfall sind Matrizen quadratisch, d.h. Zeilen- und Spaltenzahl sind gleich. Dann liefert das Produkt zweier gleichgroßer quadratischer Matrizen wiederum eine quadratische Matrix, die in Zeilen- und Spaltenzahl mit den Ausgangsmatrizen übereinstimmt.
